гӮӘгғҡгӮўгғігғ—пјҲжј”з®—еў—е№…еҷЁпјүгӮ’дҪҝгҒЈгҒҹз©ҚеҲҶеӣһи·ҜгӮ’дёӢеӣігҒ«зӨәгҒ—гҒҫгҒҷгҖӮеҸҚи»ўеў—е№…еӣһи·ҜгҒ®её°йӮ„жҠөжҠ— \(R_f\) гӮ’гӮігғігғҮгғігӮө \(C\) гҒ§зҪ®гҒҚжҸӣгҒҲгҒҹеҪўгӮ’гҒ—гҒҰгҒ„гҒҫгҒҷгҖӮ
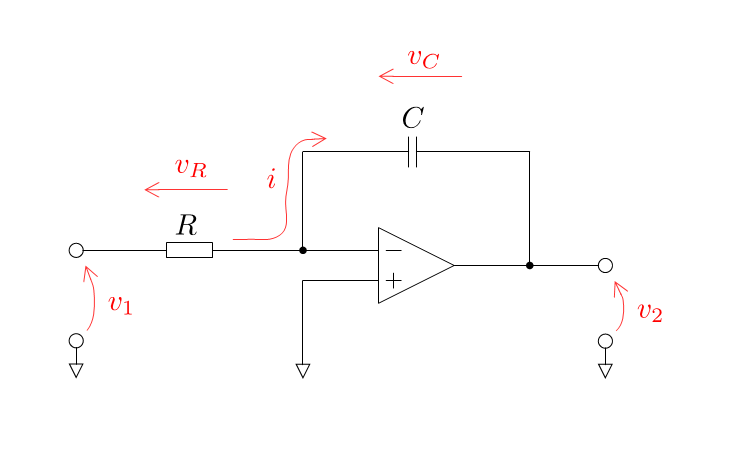
з©ҚеҲҶеӣһи·ҜгҒ®е…ҘеҠӣйӣ»ең§гӮ’ \(v_1\)пјҢеҮәеҠӣйӣ»ең§гӮ’ \(v_2\) гҒЁгҒ—гҒҫгҒҷгҖӮ жҠөжҠ— \(R\) гҒ«жөҒгӮҢгӮӢйӣ»жөҒгӮ’ \(i\) гҒЁгҒҷгӮӢгҒЁпјҢзҗҶжғізҡ„гҒӘгӮӘгғҡгӮўгғігғ—гҒ®е…ҘеҠӣз«ҜеӯҗгҒ«гҒҜйӣ»жөҒгҒҢжөҒгӮҢгҒӘгҒ„гҒ®гҒ§пјҢгӮігғігғҮгғігӮө \(C\) гҒ«жөҒгӮҢгӮӢйӣ»жөҒгӮӮ \(i\) гҒ§гҒҷгҖӮ гҒ“гҒ®гҒЁгҒҚпјҢжҠөжҠ— \(R\) гҒ®дёЎз«ҜгҒ«зҷәз”ҹгҒҷгӮӢйӣ»ең§гӮ’ \(v_R\)пјҢгӮігғігғҮгғігӮө \(C\) гҒ®дёЎз«ҜгҒ«зҷәз”ҹгҒҷгӮӢйӣ»ең§гӮ’ \(v_C\) гҒЁгҒ—гҒҫгҒҷгҖӮ
гӮӘгғҡгӮўгғігғ—гҒ®е…ҘеҠӣз«Ҝеӯҗй–“гҒ«гғҗгғјгғҒгғЈгғ«гӮ·гғ§гғјгғҲпјҲд»®жғізҹӯзөЎпјүгӮ’д»®е®ҡгҒҷгӮӢгҒЁпјҢеҸҚи»ўе…ҘеҠӣз«ҜеӯҗгҒ®йӣ»дҪҚгҒҜ \(\rm 0\) гҒ§гҒҷгҖӮ гӮҲгҒЈгҒҰпјҢж¬ЎгҒ®ејҸгҒҢжҲҗгӮҠз«ӢгҒЎгҒҫгҒҷгҖӮ $$ v_1 = v_R = i R $$ гҒ“гӮҢгҒӢгӮүпјҢ $$ i = \frac{v_1}{R} $$ гҒ§гҒҷгҖӮ гҒҫгҒҹпјҢ $$ v_2 + v_C = 0 $$ гӮӮжҲҗгӮҠз«ӢгҒӨгҒ®гҒ§пјҢ $$ v_2 = - v_C $$ гҒ§гҒҷгҖӮгҒ“гҒ“гҒ§пјҢ\(v_C\) гҒҜгӮігғігғҮгғігӮө \(C\) гҒ«и“„гҒҲгӮүгӮҢгҒҰгҒ„гӮӢйӣ»иҚ· \(q\) гӮ’дҪҝгҒЈгҒҰж¬ЎејҸгҒ§иЎЁгҒҷгҒ“гҒЁгҒҢгҒ§гҒҚгҒҫгҒҷгҖӮ $$ v_C = \frac{q}{C} $$ гҒ•гӮүгҒ«пјҢгӮігғігғҮгғігӮөгҒ«и“„гҒҲгӮүгӮҢгҒҹйӣ»иҚ· \(q\) гҒҜгӮігғігғҮгғігӮөгҒ«жөҒгӮҢгҒҹйӣ»жөҒ \(i\) гӮ’з©ҚеҲҶгҒ—гҒҹгӮӮгҒ®гҒӘгҒ®гҒ§пјҢ\(t=0\) гҒ«гҒҠгҒ‘гӮӢйӣ»иҚ·гӮ’ \(0\) гҒЁгҒҷгӮӢгҒЁпјҢж¬ЎејҸгҒ§иЎЁгҒӣгҒҫгҒҷгҖӮ $$ q(t) = \int_0^t i(t) dt $$ д»ҘдёҠгҒӢгӮүпјҢ $$ v_2(t) = - v_C(t) = -\frac{q(t)}{C} = -\frac{1}{C} \int_0^t i(t) dt = -\frac{1}{C} \int_0^t \frac{v(t)}{R} dt $$ гҒЁгҒӘгҒЈгҒҰпјҢзөҗеұҖ $$ v_2(t) = -\frac{1}{CR} \int_0^t v_1(t) dt $$ гҒЁжӣёгҒ‘гҒҫгҒҷгҖӮгҒӨгҒҫгӮҠпјҢз©ҚеҲҶеӣһи·ҜгҒҜгҒқгҒ®еҗҚгҒ®йҖҡгӮҠпјҢеҮәеҠӣйӣ»ең§ \(v_2\) гҒҢе…ҘеҠӣйӣ»ең§ \(v_1\) гӮ’з©ҚеҲҶгҒ—гҒҹгӮӮгҒ®гҒ«жҜ”дҫӢгҒ—гҒҫгҒҷгҖӮ
зү№еҲҘгҒӘе ҙеҗҲгҒЁгҒ—гҒҰпјҢе…ҘеҠӣйӣ»ең§ \(v_1\) гҒҢжҷӮй–“гҒ«гӮҲгӮүгҒҡдёҖе®ҡгҒ®е ҙеҗҲгӮ’иҖғгҒҲгҒҰгҒҝгҒҫгҒҷгҖӮ $$ v_1(t) = V_1 $$ гҒЁгҒҷгӮӢгҒЁпјҢ $$ v_2(t) = -\frac{1}{CR} \int_0^t V_1 dt = -\frac{V_1}{CR}t $$ гҒЁжӣёгҒ‘гҒҫгҒҷгҖӮгҒӨгҒҫгӮҠпјҢеҮәеҠӣйӣ»ең§гҒҜеӮҫгҒҚгҒҢ \(-\frac{V_1}{CR}\) гҒ®зӣҙз·ҡзҠ¶гҒ«гҒӘгӮҠгҒҫгҒҷгҖӮ